A lo largo de este artículo, te explicaremos la importancia de la denominada Ley del Minimo o Ley de Liebig en la nutrición vegetal. Para ello, comenzaremos por aclarar qué es la ley del minimo y qué nos enseña acerca del uso de los recursos para, posteriormente, relacionarla con la nutrición vegetal.
La Ley del Minimo de Liebig
En un concepto restringido, la fertilidad es considerada como la capacidad del suelo para suministrar a las plantas los elementos nutritivos esenciales para su crecimiento. Sobre la base de este concepto se han desarrollado diversas leyes y teorías fundamentales de las relaciones entre el crecimiento de las plantas y el suministro de elementos nutritivos. Aunque han surgido nuevas teorías y modelos, estas relaciones aún son la base para numerosas evaluaciones del estado de fertilidad de los suelos, destacándose entre ellas la que se conoce como Ley del Mínimo de Liebig.
La Ley del Mínimo también es conocida como Ley de Liebig, aunque Carl Sprengel, un botánico alemán (1787-1859), estudioso y profesor universitario, fue el primero en formular la “Teoría del Mínimo” en química agrícola, con el significado de que el crecimiento de las plantas es limitado por el nutriente esencial a la más baja concentración. Esta regla, frecuentemente e incorrectamente atribuida a Justus von Liebig como la “Ley del Mínimo de Liebig”, fue solamente popularizada por éste, un químico alemán (1803-1873) pionero del desarrollo de la química agrícola, como un concepto científico: el crecimiento no es controlado por el monto total de los recursos disponibles, si no por el recurso más escaso.
Ese concepto se aplicó originalmente al crecimiento de las plantas en función de la disponibilidad de nutrientes, donde se encontró que el aumento de la cantidad del nutriente más abundante no hace aumentar el crecimiento de las plantas, y solo mediante el aumento de la cantidad del nutriente limitante se puede mejorar el crecimiento vegetal (Te podría interesar: Ley del mínimo de Liebig: ¿Es importante para tu empresa? ).
La representacion grafica de la Ley del Minimo de Liebig
Liebig representó este concepto con un barril que contiene un líquido, dicho barril está formado por duelas de diferentes tamaños y cada duela representa un nutriente esencial. De esta manera, al tratar de llenar el barril, el líquido se derramará por la duela más corta y no se puede llenar más allá de este límite; así mismo, la planta no crecerá más allá de lo que permita la insuficiencia de ese nutriente, representado por la duela más corta, por ser el que se encuentra en menor proporción en un suelo determinado.
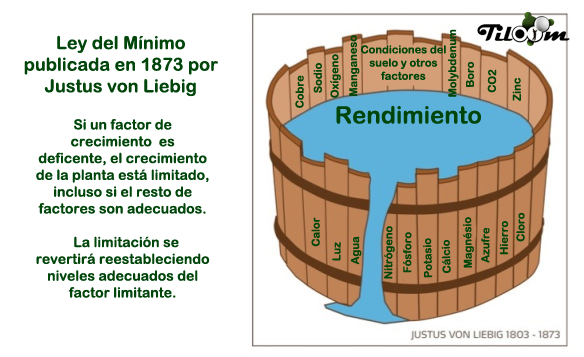
Entonces el crecimiento de una planta va a estar limitado por el elemento nutritivo esencial que se encuentre en menor proporción en el medio donde se desarrolla la planta. Lógicamente, esta limitación en el crecimiento de la planta, ocurrirá siempre y cuando la cantidad aprovechable de ese elemento esencial se encuentre en niveles de insuficiencia.
La Ley de los Incrementos Decrecientes en la Nutricion Vegetal
Esta teoría del mínimo de Sprengel, popularizada y ampliada por Liebig, ha inspirado otras teorías relativas a la nutrición vegetal. Es el caso de la “Ley de los Incrementos Decrecientes” formulada por Mitscherlich, quien la enunció sobre la base de que las plantas, cuando disponen de adecuadas cantidades de nutrientes con la excepción de uno de ellos, su crecimiento estará limitado por ese factor (Te podría interesar: Ley del Mínimo o Ley de Liebig – Fertilización de cultivos).
Un incremento en la cantidad de ese elemento limitante provocará un incremento en el crecimiento de las plantas. Ésta no es una simple relación lineal, ya que ha sido demostrado que la adición de cada unidad sucesiva de un factor de crecimiento, resulta en un incremento en el crecimiento de la planta que es menor al obtenido con la adición de las unidades precedentes. Esto lo expresó Mitscherlich en su ecuación:
dy/dx = (A-y)C
donde:
dy=Incremento en cosecha como resultado de un incremento en el factor de crecimiento dx.
dx=Incremento del factor de crecimiento.
A=Máximo de cosecha obtenible suministrando todos los factores de crecimiento en cantidades óptimas.
y=Cosecha obtenida después de aplicar el factor x.
C=Constante de proporcionalidad dependiente de la naturaleza del factor de crecimiento.
Según Mitscherlich, C=0,122 para N
C=0,60 para P2O5
C=0,40 para K2O
Posteriormente, Spillman expresó la relación entre crecimiento y el factor de crecimiento de la siguiente manera:
y=M(1-Rx)
Más adelante, Spillman mostró que su ecuación y la de Mitscherlich podían reducirse a la siguiente forma:
y=A(1-10-cx)
Una forma equivalente de estas expresiones es:
log(A-y)=logA-0,301(x)
En este caso A es el rendimiento en función del factor de crecimiento x, pero el rendimiento expresado en forma relativa, de tal manera que A=100 y el valor 0,301 reemplaza la constante C. De esta forma, la ecuación se reduce a:
log(100-y)=log100 – 0,301(x)
Si el factor de crecimiento está totalmente ausente, entonces x=0, y consecuentemente y=0. Si añadimos una unidad del factor x, entonces x=1 y el rendimiento esperado es:
log(100-y)=log100 – 0,301(1)
log(100-y)=2 – 0,301
log(100-y)=1,699
100-y=50
y=50
Lo que indica que cuando se añade una unidad de x se obtiene un rendimiento que es 50% del máximo. Al añadir dos unidades del factor x, entonces x=2 y el rendimiento esperado es:
log(100-y)=log100 – 0,301(2)
log(100-y)=2 – 0,602
log(100-y)=1,398
100-y=25
y=75
Realizando la misma operación hasta 10 unidades del factor de crecimiento x, se aprecia que incrementos sucesivos de un factor de crecimiento (por ejemplo, un nutriente esencial) resultan en un incremento del rendimiento que es 50% del incremento obtenido con la adición de la unidad precedente, hasta que se llega a un punto en el cual los incrementos logrados con cada unidad adicional del factor de crecimiento son insignificantes, tienden a cero.
Esta relación matemática es interesante si aceptamos su validez, porque muestra claramente que cuando se aplican dosis de fertilizantes muy altas o excesivas, es posible que los incrementos logrados en rendimiento no compensen el incremento en costo del fertilizante. Es decir, puede ocurrir que el incremento en costo de producción por el incremento en la dosis del fertilizante sea mayor que el incremento en el valor de la producción alcanzada, o lo que es lo mismo, se tiende a lograr el máximo rendimiento biológico posible pero se tiende a sobrepasar lo que se conoce como “máximo rendimiento económico”, con la consecuente disminución del retorno neto.
Actualmente se denomina Disponibilidades Óptimas Agronómicas (DOA) a la cantidad de nutriente necesaria para alcanzar el rendimiento máximo y Disponibilidades Óptimas Económicas (DOE) a la cantidad de nutriente necesaria para alcanzar el máximo retorno económico al fertilizar.
Todas estas teorías tienen limitaciones ya que además de las interacciones entre los nutrientes hay otros factores que afectan las curvas de rendimiento, como son los factores ambientales y sus interacciones con los nutrientes del suelo, lo cual es muy particular para cada sistema suelo-planta-clima. Así por ejemplo, si un cultivo no dispone de humedad adecuada, la aplicación de una cantidad X de un fertilizante originará un rendimiento más bajo que con una humedad edáfica adecuada; si el suelo es ácido o no, la respuesta será igualmente diferente, etc.
A pesar de sus limitaciones, a todos esos conceptos debe dársele la debida consideración, porque representan un intento original de desarrollar una teoría del crecimiento de las plantas como una función de la nutrición mineral. Es indudable que el crecimiento de las plantas como una función de la aplicación de nutrientes sigue un patrón de incrementos decrecientes como lo señala la ecuación de Mitscherlich. Igualmente, el crecimiento de una planta anual tiende a alcanzar un máximo con incrementos en la aplicación de nutrientes, bajo determinadas condiciones ambientales.
Entonces, lo que refleja la Ley del Minimo de Liebig es que SIN FERTILIZANTES es imposible producir la cantidad de alimentos que necesitamos para satisfacer los requerimientos de la población.



